By: Renaissance Professional Development Team

The third and final post in our series of blogs following our webinar on Guiding Effective Literacy and Numeracy Teaching explores three exciting numeracy strategies!  Keep in mind, these are all compatible in both arenas, there’s certainly a place for these strategies in a reading lesson, just as the others can be applied to numeracy teaching too. Let’s get straight into it!

PRE AND POST TESTING

Pre and post tests are designed to measure your students’ growth in knowledge of a particular topic.  Not only do they assist in measuring how your students have improved, but they can also be a valuable diagnostic tool for more effective teaching as well. This can operate on many different levels in the classroom. It may be a question you give at the start and end of the lesson. It might be more detailed and over a greater period of time though.

For example, a Stage 2 teacher might have a unit of work for the term on Numbers and Algebra. They may choose to present students with a pre-test consisting of number sentences involving addition and subtraction and number patterns using multiples. When administering these pre-tests in the classroom, it is crucial that students aware that the first test is to work out what they already know. Ensuring they know that the teacher is not overly concerned about the score of this test, but rather finding out their prior knowledge. This assessment could also be used to inform individual student goals down the track.  

Once having taught the topic or the strategy of attacking that particular type of problem explicitly, students would sit the same or very similar post-test to ascertain their growth. On a side note, in a perfect world, a student would not answer any question they did not know the answer to. As teachers, we need to account for the natural tendency to answer every question so researchers conducted pre and post testing with a qualifying question, simply adding to each a tick a box underneath with “yes I know the answer” or “I am guessing” which provides us with an ever greater depth of knowledge on the student’s ability. The teacher is also in a position to offer feedback after the pre-test to inform the student’s approach in the coming lessons.  

REFLECTION ON FEEDBACK 

In our various discussions with schools, we’ve found some are having great success with encourage students to ‘think about your thinking’ as part of their habits of mind. It has been said that “learning comes about not from just doing, but from thinking about what we do” – the metacognition.[1]  Students reflecting on the feedback given to them in an assessment task or any activity, creates an important part of student learning cycle.

Kolb’s Learning Cycle proposes that the opportunity for students to reflect on learning experiences is vital to the learning cycle process. By encouraging students to reflect on the tasks they have been assessed in, they are no longer just focused on the ‘how’ of their task, – but the ‘why’ of that assessment task. In doing so, they become aware of the numeracy skills that they have developed and, the ones that require some more refining.[2]

Reflection on assessment feedback[3] can have a high impact on the student numeracy learning cycle when: 

• feedback is timely, regular and relevant to the learning
• There is time to receive, reflect and act upon feedback
• Feedback is provided as a guide for learning, not just as assessment in itself
• Students understand the feedback and purpose of the feedback
• What students need to do in order to improve that skill
• Marking rubrics are included as part of the assessment process

Teachers might use tools to provide feedback, such as a type of digital interaction found in a numeracy practice software program or a learning management system.

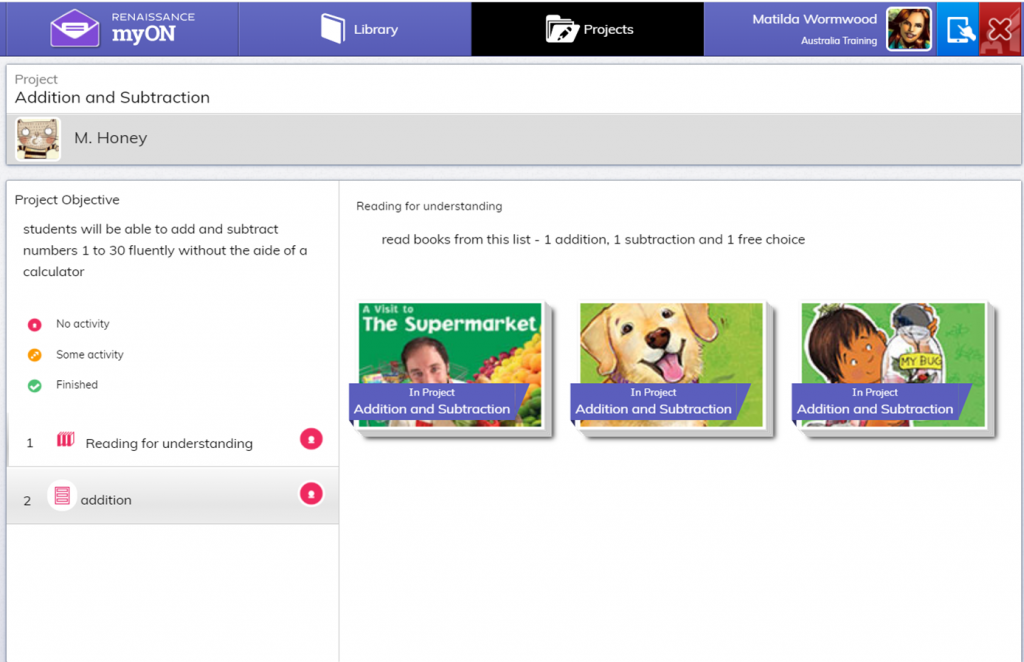
Assessment feedback in numeracy, aids in the students understanding of the mathematical concept and skill, and what they need to do to succeed.  The understanding of the feedback can be regarded as the student’s backbone of reflecting on their work to achieve learning goals. One such example of this can be found in Math based projects created in myON.

Teachers give feedback on the Math task, where students then reflect on the teacher feedback in a written task that is also part of the project. 

LEARNING STYLES

As mentioned previously, the strategies discussed here are applicable across both literacy and numeracy and this is especially evident with learning styles. The seven most common learning styles you may have seen mentioned online and in textbooks are:[4]

• Visual
• Aural
• Verbal
• Kinaesthetic
• Logical
• Social 
• Solitary 
•  

It’s important to remember that we all have teaching styles that will lean one way or another depending on personal preference/practice and this will influence lesson planning, so who might we leave behind if we stick to the same learning/teaching styles over and over again? Understandably, with large classes and busy schedules it’s not always possible to a) identify what types of learners all students are, and b) personalise lesson. 

With all of that said, interestingly in the context of the Mathematics classroom, Silver, Thomas, and Perini found that there are actually 4 distinct learning styles.[5]

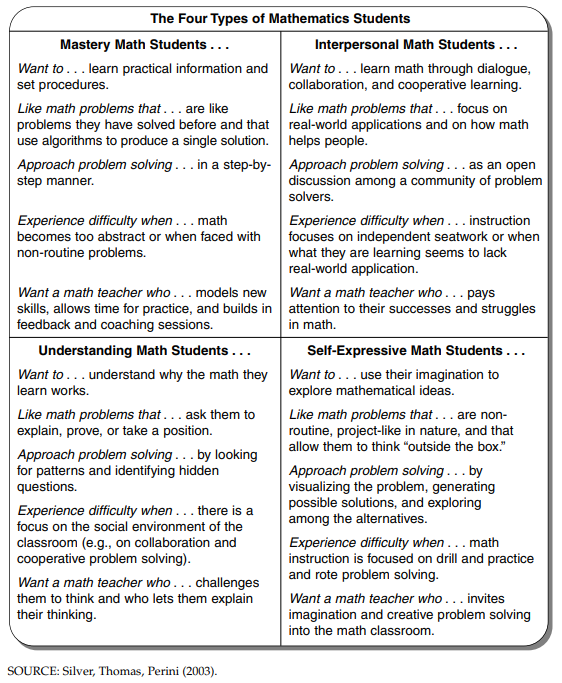
They also found that no student fell completely into one style or category.  One of the ways to address these 4 different learning styles in the mathematics classroom is to integrate activities across a unit of study that utilise all of them. Now you’re possibly thinking, I’m a busy person with lots to do, I don’t have time to identify each student’s learning style and then cater to each student in every lesson but what if over the course of the unit on area and perimeter, students covered all 4 learning styles in activities? We get a differentiated mathematics classroom, one in which every learner gets what he or she needs, while also growing underdeveloped capacities by working in styles where they may be weaker. 

By following this strategy, we can ask students across the unit of study to complete any activity that asks them to:  

• Apply formulas, compute accurately, and reinforce skills through practice (Mastery)
• Discover patterns, make estimates, and develop mathematically sound explanations (Understanding)
• Think creatively, develop new problems, and try out a variety of problem-solving approaches (Self-Expressive) 
• Make personal connections and solve real-world math problems (Interpersonal)

Style-based mathematics instruction is more than a way to invite a greater number of students into the teaching and learning process. It is also a way to ensure high performance from students. Sternberg found that whenever students were taught in a way that matched their own style preferences, those students outperformed students who were mismatched. Following this, it was also found that students who were taught using a diversity of approaches outperformed all other students on both performance assessments and on multiple-choice memory tests.  

Organising maths lessons by style can make the work of differentiating instruction and assessment for every learner a manageable task.  

As you can imagine, this is only a small peek into the world of numeracy. The Renaissance Team is always looking for new and exciting information to bring to you. Why not take a look at Freckle? Renaissance’s latest offering is an incredible math practice solution offering each student the right level of challenge and guided instruction for students looking to develop and strengthen their mathematic understanding and capability. Get in touch for more information!

To learn more about how you can accelerate your schools numeracy CLICK HERE!

Referencing: 

[1] http://www.ascd.org/publications/books/108008/chapters/Learning-Through-Reflection.aspx

[2] https://www.simplypsychology.org/learning-kolb.html

[3] https://education.nsw.gov.au/teaching-and-learning/school-learning-environments-and-change/future-focused-learning-and-teaching/learning-modes/feedback-and-reflection

[4] https://www.time4learning.com/learning-styles/

[5] https://www.corwin.com/sites/default/files/upm-binaries/19562_Chapter_1.pdf

Share on Facebook

Tweet

Follow us